Skip to main content

Section 1.1 Complete Chaos is Impossible

Complete disorder is impossible. — Theodore S. Motzkin, Israeli-American mathematician, 1908 — 1970.

What is Ramsey theory?

  • Ramsey theory is the mathematics of colouring. - Soifer

  • Ramsey theory is the study of the preservation of properties under set partitions. - Landman-Robertson

  • The fundamental kind of question Ramsey theory asks is: can one always find order in chaos? If so, how much? Just how large a slice of chaos do we need to be sure to find a particular amount of order in it? - Leader

  • If mathematics is a science of patterns, then Ramsey theory is a science of the stubbornness of patterns. - Jungic

Example 1.1.1.

A Ramsey theory problem: If the natural numbers are finitely coloured, i.e. the set of natural numbers is partitioned into a finite number of cells, must there exist \(x\text{,}\) \(y\) (with \(x\) and \(y\) not both equal to 2) with \(x + y\) and \(xy\) monochromatic, i.e., \(x + y\) and \(xy\) belong to the same partition cell? (See Figure 1.1.2.)

Figure 1.1.2. Monochromatic pattern?

The problem was posed by Neil Hindman in the late 1970s and resolved by Joel Moreira in 2017: Monochromatic sums and products in \(\mathbb{N}\text{,}\) Annals of Mathematics (2) 185 (2017), no. 3, 1069–1090. [ arXiv]

What makes this problem to be a typical Ramsey theory problem is the following:

  • The topic: the problem is to determine the relationship between the set of all finite partitions of the natural numbers and a certain pattern.

  • The fact that any numerically literate person can understand the problem.

  • It is a difficult problem.

Example 1.1.3.

Schur's Theorem: For any partition of the positive integers into a finite number of parts, one of the parts contains three integers \(x, y, z\) with \(x + y = z\text{.}\) (See Figure 1.1.5.)

Figure 1.1.4. Issai Schur (1875 — 1941)

Figure 1.1.5. True, by Schur's theorem

Example 1.1.6.

van der Waerden's Theorem - Special Case. For any partition of the positive integers into a finite number of parts, one of the parts contains three integers \(x, y, z\) with \(x + y = 2z\text{.}\) (See Figure 1.1.8.)

Figure 1.1.7. Bartel Leendert van der Waerden (1903 — 1996)

Figure 1.1.8. True, by van der Waerden's theorem

Example 1.1.9.

Rado's Theorem - Special Case. For any partition of the positive integers into a finite number of parts, one of the parts contains three integers \(x,y, z\) with \(ax + by + cz=0\text{,}\) \(a\not =0\text{,}\) \(b\not=0\text{,}\) \(c\not=0\text{,}\) if and only if one of the following conditions holds \(a+b+c=0\) or \(a+b=0\) or \(a+c=0\) or \(b+c=0\text{.}\) (See Figure 1.1.11.)

Figure 1.1.10. Richard Rado (1906 — 1989)

Figure 1.1.11. True, by Rado's theorem

Example 1.1.12.

Ramsey's Theorem - Special case. If there are at least six people at dinner then either there are three mutual acquaintances or there are three mutual strangers. (See Figure 1.1.14.)

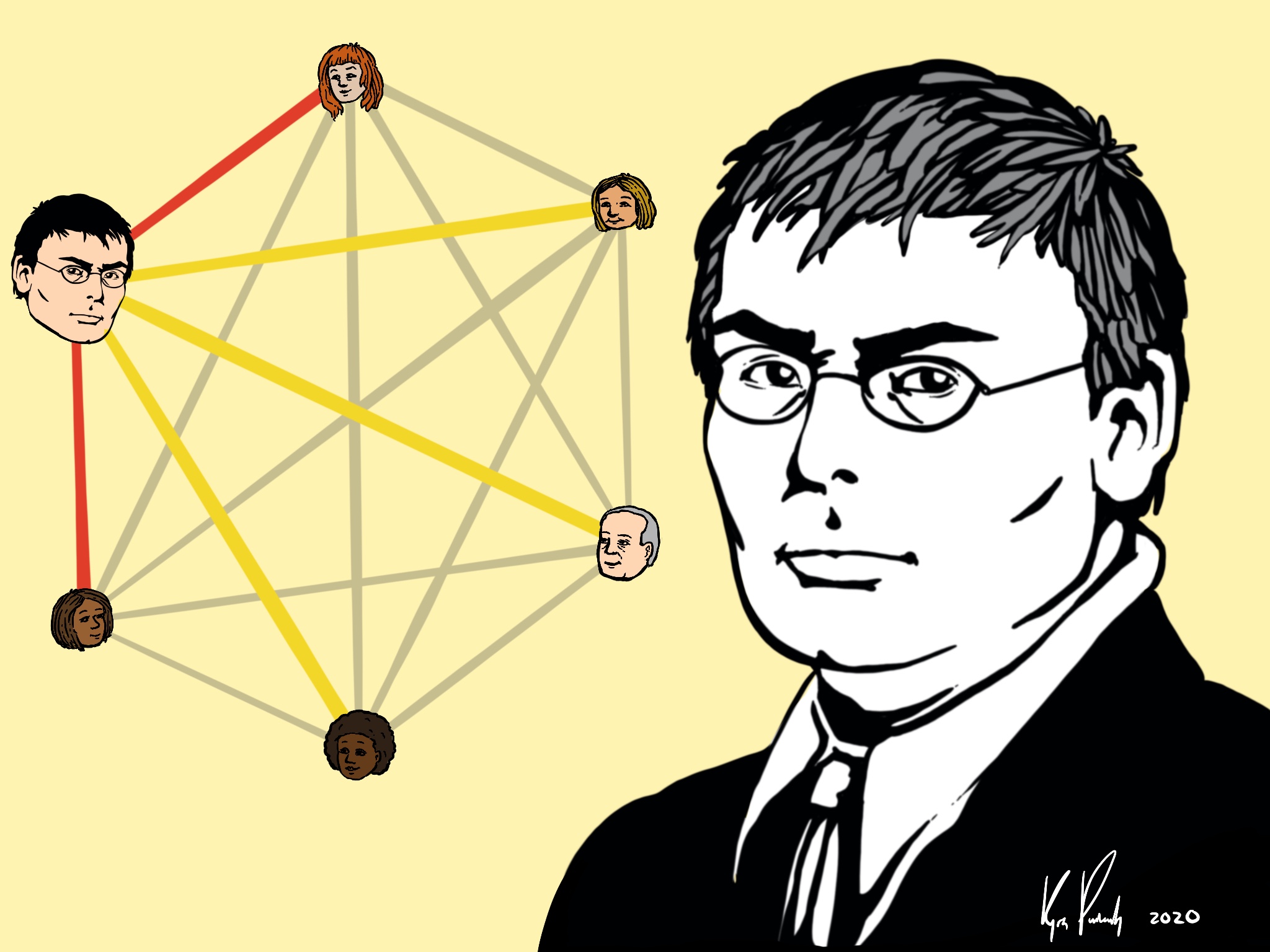
Figure 1.1.13. Frank Plumpton Ramsey (1903 — 1930)

Figure 1.1.14. Proof of a special case of Ramsey's theorem.

Example 1.1.15.

Hales-Jewett Theorem - Informal. In large enough dimensions, the game of Tic-Tac-Toe cannot end in a draw.

Figure 1.1.16. Alfred Hales and Robert Jewett

Figure 1.1.17. Tic-Tac-Toe

Tic-Tac-Toe - It is a win!

\begin{equation*} \begin{array}{ccccccccccc} 11\amp 12\amp \color{red}{13}\amp \ \amp 11\amp 12\amp 13\amp \amp \color{red}{11}\amp 12\amp 13\\ 21\amp 22\amp \color{red}{23}\amp \mbox{ or } \amp \color{red}{21}\amp \color{red}{22}\amp \color{red}{23}\amp \mbox{ or } \amp 21\amp \color{red}{22}\amp 23\\ 31\amp 32\amp \color{red}{33}\amp \ \amp 31\amp 32\amp 33\amp \amp 31\amp 32\amp \color{red}{33} \end{array} \end{equation*}

Resources.

  1. See [2], [3], and [7].

  2. Ramsey Theory - Wikipedia

  3. Ramsey Theory by R. Graham and B. Rothschild

  4. Ramsey Theory by J. Fox